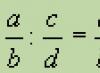В этой статье мы начнем изучать рациональные числа . Здесь мы дадим определения рациональных чисел, дадим необходимые пояснения и приведем примеры рациональных чисел. После этого остановимся на том, как определить, является ли данное число рациональным или нет.

Навигация по странице.

Определение и примеры рациональных чисел

В этом пункте мы дадим несколько определений рациональных чисел. Несмотря на различия в формулировках, все эти определения имеют единый смысл: рациональные числа объединяют целые числа и дробные числа , подобно тому, как целые числа объединяют натуральные числа , противоположные им числа и число нуль. Иными словами, рациональные числа обобщают целые и дробные числа.

Начнем с определения рациональных чисел , которое воспринимается наиболее естественно.

Из озвученного определения следует, что рациональным числом является:

• Любое натуральное число n . Действительно, можно представить любое натуральное число в виде обыкновенной дроби , например, 3=3/1 .
• Любое целое число, в частности, число нуль. В самом деле, любое целое число можно записать в виде либо положительной обыкновенной дроби, либо в виде отрицательной обыкновенной дроби, либо как нуль. Например, 26=26/1 , .
• Любая обыкновенная дробь (положительная или отрицательная). Это напрямую утверждается приведенным определением рациональных чисел.
• Любое смешанное число . Действительно, всегда можно представить смешанное число в виде неправильной обыкновенной дроби. Например, и .
• Любая конечная десятичная дробь или бесконечная периодическая дробь . Это так в силу того, что указанные десятичные дроби переводятся в обыкновенные дроби. К примеру, , а 0,(3)=1/3 .

Также понятно, что любая бесконечная непериодическая десятичная дробь НЕ является рациональным числом, так как она не может быть представлена в виде обыкновенной дроби.

Теперь мы можем с легкостью привести примеры рациональных чисел . Числа 4 , 903 , 100 321 – это рациональные числа, так как они натуральные. Целые числа 58 , −72 , 0 , −833 333 333 тоже являются примерами рациональных чисел. Обыкновенные дроби 4/9 , 99/3 , - это тоже примеры рациональных чисел. Рациональными числами являются и числа .

Из приведенных примеров видно, что существуют и положительные и отрицательные рациональные числа, а рациональное число нуль не является ни положительным, ни отрицательным.

Озвученное выше определение рациональных чисел можно сформулировать более краткой форме.

Определение.

Рациональными числами называют числа, которые можно записать в виде дроби z/n , где z – целое число, а n – натуральное число.

Докажем, что данное определение рациональных чисел равносильно предыдущему определению. Мы знаем, что можно рассматривать черту дроби как знак деления , тогда из свойств деления целых чисел и правил деления целых чисел следует справедливость следующих равенств и . Таким образом, , что и является доказательством.

Приведем примеры рациональных чисел, основываясь на данном определении. Числа −5 , 0 , 3 , и являются рациональными числами, так как они могут быть записаны в виде дробей с целым числителем и натуральным знаменателем вида и соответственно.

Определение рациональных чисел можно дать и в следующей формулировке.

Определение.

Рациональные числа – это числа, которые могут быть записаны в виде конечной или бесконечной периодической десятичной дроби.

Это определение также равносильно первому определению, так как всякой обыкновенной дроби соответствует конечная или периодическая десятичная дробь и обратно, а любому целому числу можно сопоставить десятичную дробь с нулями после запятой.

Например, числа 5 , 0 , −13 , представляют собой примеры рациональных чисел, так как их можно записать в виде следующих десятичных дробей 5,0 , 0,0 , −13,0 , 0,8 и −7,(18) .

Закончим теорию этого пункта следующими утверждениями:

• целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел;
• каждое рациональное число может быть представлено в виде дроби с целым числителем и натуральным знаменателем, а каждая такая дробь представляет собой некоторое рациональное число;
• каждое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби, а каждая такая дробь представляет собой некоторое рациональное число.

Является ли данное число рациональным?

В предыдущем пункте мы выяснили, что любое натуральное число, любое целое число, любая обыкновенная дробь, любое смешанное число, любая конечная десятичная дробь, а также любая периодическая десятичная дробь является рациональным числом. Это знание нам позволяет «узнавать» рациональные числа из множества написанных чисел.

Но как быть, если число задано в виде некоторого , или как , и т.п., как ответить на вопрос, является ли данное число рациональным? Во многих случаях ответить на него очень сложно. Укажем некоторые направления ходу мысли.

Если число задано в виде числового выражения, которое содержит лишь рациональные числа и знаки арифметических действий (+, −, · и:), то значение этого выражения представляет собой рациональное число. Это следует из того, как определены действия с рациональными числами . Например, выполнив все действия в выражении , мы получаем рациональное число 18 .

Иногда, после упрощения выражений и более сложного вида, появляется возможность определить, рационально ли заданное число.

Пойдем дальше. Число 2 является рациональным числом, так как любое натуральное число является рациональным. А как насчет числа ? Является ли оно рациональным? Оказывается, что нет, - не является рациональным числом, это иррациональное число (доказательство этого факта методом от противного приведено в учебнике по алгебре за 8 класс, указанном ниже в списке литературы). Также доказано, что квадратный корень из натурального числа является рациональным числом только в тех случаях, когда под корнем находится число, являющееся полным квадратом некоторого натурального числа. Например, и - рациональные числа, так как 81=9 2 и 1 024=32 2 , а числа и не являются рациональными, так как числа 7 и 199 не являются полными квадратами натуральных чисел.

А число рационально или нет? В данном случае несложно заметить, что , следовательно, данное число – рациональное. А является ли число рациональным? Доказано, что корень k-ой степени из целого числа является рациональным числом только тогда, когда число под знаком корня является k-ой степенью некоторого целого числа. Поэтому не является рациональным числом, так как не существует целого числа, пятая степень которого равна 121 .

Метод от противного позволяет доказывать, что логарифмы некоторых чисел по некоторым основаниям не являются рациональными числами. Для примера докажем, что - не рациональное число.

Предположим противное, то есть, допустим, что - рациональное число и его можно записать в виде обыкновенной дроби m/n . Тогда и дают следующие равенства: . Последнее равенство невозможно, так как в левой его части находится нечетное число 5 n , а в правой части – четное число 2 m . Следовательно, наше предположение неверно, таким образом, не является рациональным числом.

В заключение стоит особо отметить, что при выяснении рациональности или иррациональности чисел следует воздержаться от скоропостижных выводов.

Например, не стоит сразу утверждать, что произведение иррациональных чисел π и e является иррациональным числом, это «как бы очевидно», но не доказано. При этом возникает вопрос: «А с чего бы произведению быть рациональным числом»? А почему бы и нет, ведь можно привести пример иррациональных чисел, произведение которых дает рациональное число: .

Также неизвестно, являются ли числа и многие другие числа рациональными или не являются таковыми. Например, существуют иррациональные числа, иррациональная степень которых является рациональным числом. Для иллюстрации приведем степень вида , основание данной степени и показатель степени не являются рациональными числами, но , а 3 – рациональное число.

Список литературы.

• Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н. Я. Виленкин и др.]. - 22-е изд., испр. - М.: Мнемозина, 2008. - 288 с.: ил. ISBN 978-5-346-00897-2.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Математика. Алгебра. Геометрия. Тригонометрия

АЛГЕБРА: Числа

2.2. Целые и рациональные числа. Проценты

Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему. Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если m кратно n).

Принято сумму натурального числа и правильной дроби записывать без знака сложения, т. е. вместо пишут . Число, записанное в таком виде, называется смешанным числом. Оно состоит из целой и дробной части.

1. Сложение обыкновенных дробей выполняется так:

а) если знаменатели одинаковые, то числители складывают и оставляют тот же знаменатель: ;

2. Вычитание обыкновенных дробей выполняется следующим образом:

а) если знаменатели одинаковые, то

3. Умножение обыкновенных дробей выполняется следующим образом:

.

Теорема 10.

2)60Ч 1,25 = 75.

Copyright © 2005-2013 Xenoid v2.0

Использование материалов сайта возможно при условии указания активной ссылки

Обыкновенная дробь - это число вида где тип - натуральные числа, например Число называется числителем дроби, - знаменателем. В частности, может быть в этом случае дробь имеет вид но чаще пишут просто Это означает, что всякое натуральное число можно представить в виде обыкновенной дроби со знаменателем 1. Запись - другой вариант записи

Среди обыкновенных дробей различают правильные и неправильные

дроби. Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.

Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь - такова, что кратно например

Пример. Представить неправильную дробь в виде суммы натурального числа и правильной дроби: а)

Решение, а)

Принято сумму натурального числа и правильной дроби записывать без знака сложения, т. е. вместо пишут вместо пишут Число, записанное в таком виде, называется смешанным числом. Оно состоит из двух частей: целой и дробной. Так, для числа 3 - целая часть равна 3, а дробная - Всякую неправильную дробь можно записать в виде смешанного числа (или в виде натурального числа). Верно и обратное: всякое смешанное или натуральное число можно записать в виде неправильной дроби. Например, .